jp armstrong

Rubik's Cube Simulator in C

Ahh the Rubik's Cube, a 6x3x3 cube game you can read about on Wikipedia. Here I'll be breaking down how I've simulated the game in C. The objective is to model a 3D object in 2D space while also letting users rotate any face either clockwise and counter clockwise.

There are a few things to consider, we need the ability to:

The cube is a 54 byte (6x9) array representing every the color of every face. A finished cube will look like the array below. Every row is a face, columns are locations of cubies on the face, and values are colors.

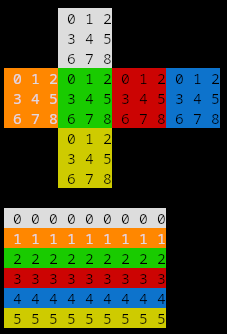
Pasted image 20240717065054

Rotation works by rotating the face and the adjacent edges. Face rotation is done by applying the mapping below to a specific row i.e. the value at index 0 is moved to 6, 1 to 3, etc. At the moment, counter clockwise rotation is done by repeating this process 3 times.

// rotation matrix
const byte F[] = {6, 3, 0, 7, 4, 1, 8, 5, 2};

Rotating the adjacent edges requires mapping out the 4 edge faces that would be at the top, right, left, and bottom of every face as well as the side of the face that's abutting the edge. The adjacency matrix is where the magic happens. Every row is a face on the cube, the columns signify the top, right, bottom, and right edges in that order.

Three types of information are encoded into a cell of the adjacency matrix:

// adjacency matrix (face and rotation: T, R, L, B)
const byte X[][4] = {
  {0x40, 0x30, 0x20, 0x10}, // U 0000
  {0x0A, 0x22, 0x52, 0x49}, // L 1001
  {0x0B, 0x32, 0x58, 0x11}, // F 1010
  {0x01, 0x4A, 0x59, 0x21}, // R 0110
  {0x00, 0x1A, 0x53, 0x39}, // B 0101
  {0x13, 0x23, 0x33, 0x43}  // D 0000
};

// adjacent edges
const byte E[][4] = {
  {0, 1, 2}, // TOP
  {2, 5, 8}, // RIGHT
  {0, 3, 6}, // LEFT
  {6, 7, 8}  // BOTTOM
};

Source code is available on github

References: